数制与编码
部分内容摘自维基百科:
1.何为数制?
数制就是一种计数法,是使用一组数字符号来表示数的体系
例:
古代人类在木头、骨头或石头上计数。
现代计算机基于二进制来进行运算和控制,计数方式相比现实中有一些区别
,计算机只能识别0和1这两种状态,计数个数(基数)为2,称为二进制计数法。
2.进位制
进位制是一种记数方式,亦称进位计数法或位值计数法。利用这种记数法,可以使用有限种数字符号来表示所有的数值。一种进位制中可以使用的数字符号的数目称为这种进位制的基数或底数。若一个进位制的基数为n,即可称之为n进位制,简称n进制。现在最常用的进位制是十进制,这种进位制通常使用10个阿拉伯数字(即0-9)进行记数。
3.数制的组成(分类)
数制是由 数码 基数 位权和计数规则组成的
数码:是数制中表示基本数值大小的不同数字符号,例如,二进制由两个数码 0 和 1 组成
基数:基数是指所使用数码的个数,例如,二进制的基数为2 十进制的基数为10
位权:位权,通俗易懂的来说,就是该数字在所处位置中的权利(价值),例如,十进制的233 2的位权是100 第一个3的位权是10 第二个3位权则是1
二进制1010 从左至右第一个位权是8 第二个位权是4 第三个位权是2 第四个位权是1
计数规则:人们使用最多的进位计数制中,表示数的符号在不同的位置上时所代表的数的值是不同的,也就是计数规则不同。
| 底/基数 | 名称 | 描述 |
|---|---|---|
| 2 | 二进制(Binary) | 几乎所有的电子计算机内部都使用二进位制,分别为“0”和“1”表示“关”和“开”。用于大多数电子计数器。 |
| 5 | 五进制 | 一般用于计算票数,“T”代表2,“正”代表5。正字一笔等于一。 |
| 8 | 八进制(Octal) | 偶尔用于计算机领域,2到3次幂。八位数字为“0-7”。 |
| 10 | 十进制(Decimal) | 世界上最常见的算术运算位进制系统,它是2和5的乘积,用于大多数机械计数器。其十位数字为 “0-9”。 |
| 12 | 十二进制 | 因为有多个约数如2,3,4和6的易于整除性,它传统上用以表示数量和总数,如一打即为十二个单位。十二位数字为“0-9”,接着是“A”和“B”。 |
| 16 | 十六进制(Hexadecimal) | 经常用于计算机领域,2到4次幂。十六位数字为“0-9”,接着是“A-F”。 |
| 20 | 二十进制 | 因为有多个约数如2,4,5和10的易于整除性,在几种传统文化中的数字系统,仍然被用于计数。二十位数字为“0-9”,接着是“A-J”。 |
| 60 | 六十进制 | 起源于古代苏美尔并传给巴比伦人。六十成为3,4和5的乘积。今天用作现代圆形坐标系(度,分,秒)和时间测量(小时,分钟和秒)的基础。 |
定点数与浮点数
计算机中机器数的类型:分为定点数(整数)与浮点数(小数)
定点数:所谓定点格式,即约定机器中所有数据的小数点位置是固定不变的。通常将定点数据表示成纯小数或纯整数,为了将数表示成纯小数,通常把小数点固定在数值部分的最高位之前;而为了将数表示成纯整数,则把小数点固定在数值部分的最后面,如下图所示:
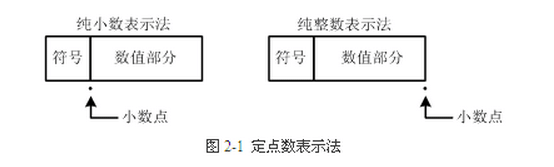
浮点数:所谓浮点数,简而言之也就是我们生活中常见的小数,浮点数由 数符、阶符、阶码、尾数组成
一个十进制数可写成一个纯小数乘上10的若干次方,相似的,一个二进制可写成一个纯小数乘上2的若干次方。
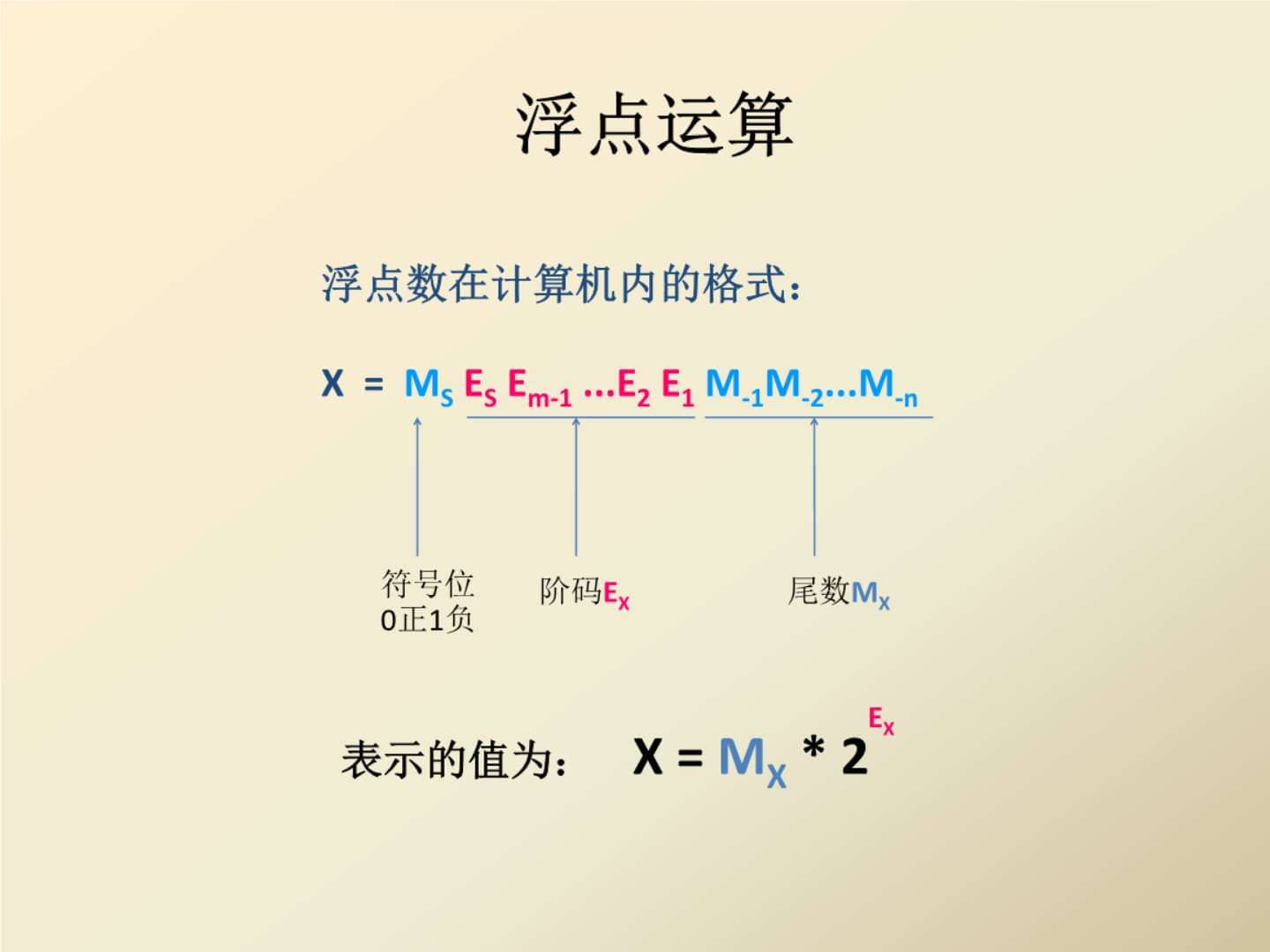
阶符:阶码的符号。
阶码:在机器中表示一个浮点数时需要给出指数,这个指数用整数形式表示,这个整数叫做阶码。
数符:数学符号,浮点表示数据格式的一个关键词。
尾数:小数点后面的数字。
4.数制转换
我们曾学习过进制转换,如十进制与二进制、八进制与二进制、二进制与十六进制的互转
回顾:
一:其它进制转换为十进制
方法是:将其它进制按权位展开,然后各项相加,就得到相应的十进制数。
二:将十进制转换成其它进制
方法是: 它是分两部分进行的即整数部分和小数部分。
整数部分:(短除法)

小数部分: (基数乘法)

三:二进制与八进制、十六进制的相互转换
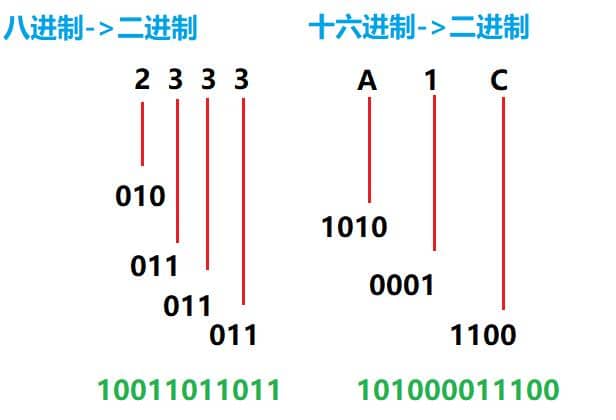
二进制转换为八进制、十六进制:它们之间满足23和24的关系,因此把要转换的二进制从低位到高位每3位或4位一组,高位不足时在有效位前面添“0”,然后把每组二进制数转换成八进制或十六进制即可
八进制、十六进制转换为二进制时,把上面的过程逆过来。
5.编码方式
二进制常用的四种编码:原码,反码,补码,移码
一. 机器数和真值
在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1、机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的,在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如,十进制中的数 +3 ,计算机字长为8位,转换成二进制就是00000011。如果是 -3 ,就是 10000011 。
那么,这里的 00000011 和 10000011 就是机器数。
2、真值
直接举例:0000 0001的真值 = +000 0001 = +1,1000 0001的真值 = –000 0001 = –1
二. 原码, 反码, 补码的基础概念和计算方法.
1. 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:
[+1]原 = 0000 0001
[-1]原 = 1000 0001
第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:
[1111 1111 , 0111 1111]
即
[-127 , 127]
原码是人脑最容易理解和计算的表示方式.
2. 反码
反码的表示方法是:
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.
[+1] = [00000001]原 = [00000001]反
[-1] = [10000001]原 = [11111110]反
可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算.
3. 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
[+1] = [00000001]原 = [00000001]反 = [00000001]补
[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
4.(扩展)移码
移码(又叫增码或偏置码)通常用于表示浮点数的阶码,其表示形式与补码相似,只是其符号位用“1”表示正数,用“0”表示负数,数值部分与补码相同。
可以理解为:移码就是将符号位取反的补码
使用移码的目的:对于一个正数和一个负数,使用移码进行比较大小之类的操作会更容易
比如 阶码为7 和-7两个值进行比较 如果直接用补码或者源码 则需要符号位即0 0000111/ 1 0000111
这样在比较浮点数的时候就要比较两次符号位 即 阶码的符号位 跟尾数的数符 对机器来说很麻烦,而如果采用移码 机器位为8的话 偏移量为2^7=127 即7=134 -7=120这样对134 跟120比较进行比较就不需要考虑符号位
6.常用编码介绍
常用字符编码:
(1)ASCII码,只有0-127,128位,使用了一个字节的低7位,剩余的128位作为扩展
(2)ISO-8859-*使用了ASCII码剩余的128位作为扩展,常用:ISO-8859-1
(3)GB2312 中文简体字集,包含6763个简体中文字
(4)Big5大五码,繁体字集
(5)Unicode统一字符集,简称UCS
(6)GBK包含GB2312和Big5简繁字集,向下完全兼容GB2312,使用GBK打开GB2312的文本不会乱码,共21003个字符
(7)UTF-8万国码,包含世界所有国家的字符
乱码
乱码,指的是由于本地计算机在用文本编辑器打开源文件时,使用了不相应字符集而造成部分或所有字符无法被阅读的一系列字符。
例:著名的"锟斤拷"[kūn jīn kǎo] 乱码
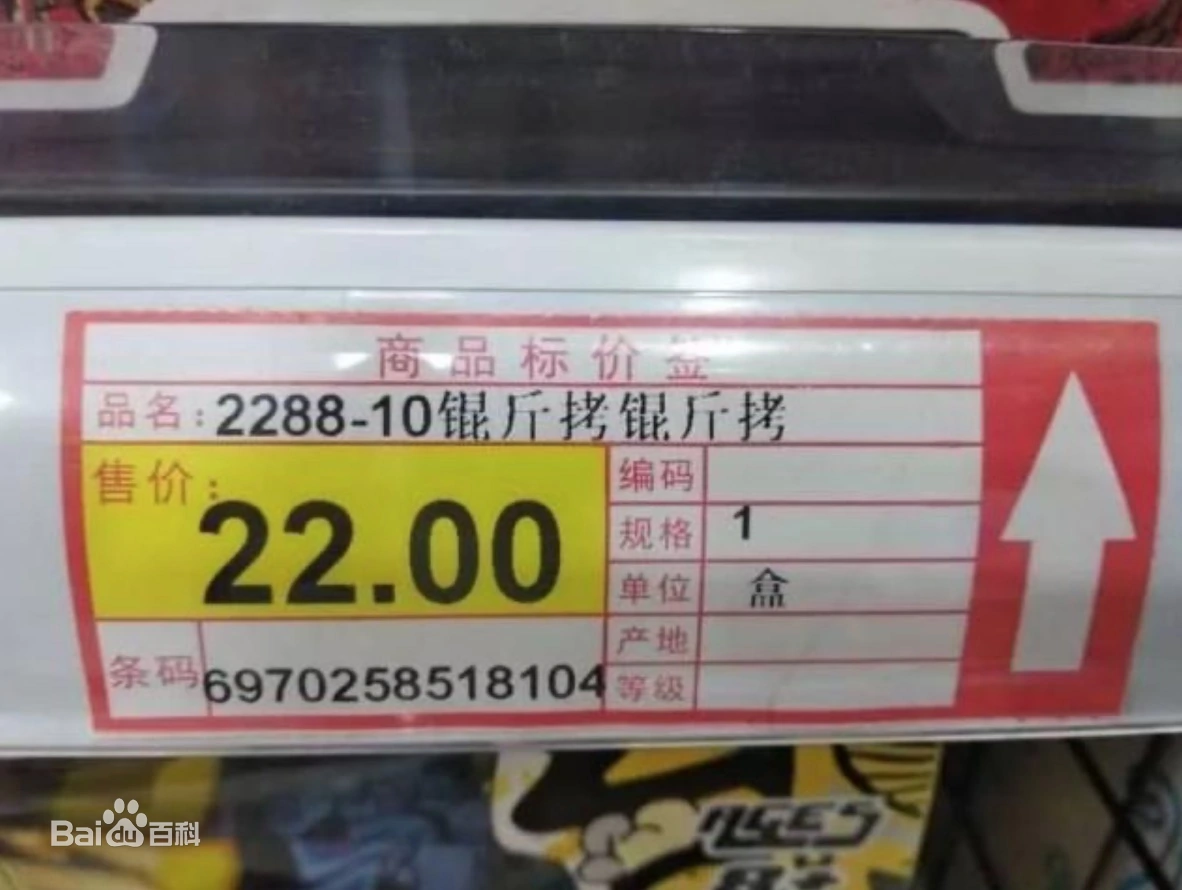
这是由于GBK字符集和Unicode字符集之间的转换错误而造成的问题